Pascal's Triangle II

Easy Array

LintCode: https://leetcode.com/problems/pascals-triangle-ii/description/

Question

Given an index k, return the kth row of the Pascal’s triangle.

For example, given k = 3,
Return [1,3,3,1].

Note:
Could you optimize your algorithm to use only O(k) extra space?

Thinking

1. What is Pascal’s Triangle? https://en.wikipedia.org/wiki/Pascal%27s_triangle
   
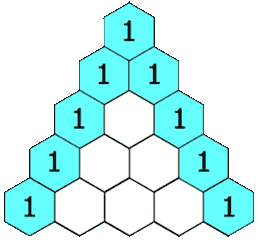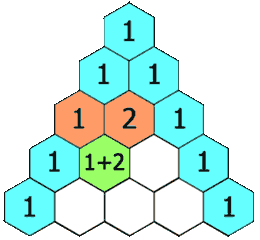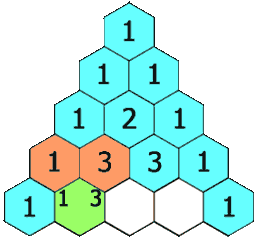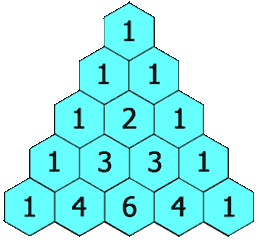
2. Pascal Triangle Coefficient (Binomial)
   
3. Formula of Binomial
   

Solution

Java

General as Pascal’s Triangle

class Solution {
    public List<Integer> getRow(int rowIndex) {
        if (rowIndex < 0) {
            throw new IllegalArgumentException("No solution");
        }
        List<Integer> res = new ArrayList<Integer>();
        if (rowIndex == 0) {
            res.add(1);
        } else if (rowIndex == 1) {
            res.add(1);
            res.add(1);
        } else if (rowIndex > 1) {
            int[] preRes = new int[]{1, 1};
            int index = 2;
            while (index <= rowIndex) {
                int[] newRes = new int[index + 1];
                newRes[0] = newRes[index] = 1;
                for (int i = 1; i < index; i ++) {
                    newRes[i] = preRes[i - 1] + preRes[i];
                }
                preRes = newRes;
                ++index;
            }
            for (int i = 0; i <= rowIndex; i++) {
                res.add(preRes[i]);
            }
        }
        return res;
    }
}

Binomial

class Solution {
    public List<Integer> getRow(int rowIndex) {
        if (rowIndex < 0) {
            throw new IllegalArgumentException("No solution");
        }
        Integer[] values = new Integer[rowIndex + 1];
        values[0] = 1;
        for (int i = 1; i < values.length; i++) {
            values[i] = (int)((long)values[i - 1] * (rowIndex - i + 1) / i);
        }
        return Arrays.asList(values);
    }
}